Malo Kerebel

Le pendule parfait est l'un des premier objets que l'on étudie en mécanique, son mouvement est prédit parfaitement par la mécanique newtonienne et donc facile à comprendre.

On cherche dans ce projet à modéliser un pendule amorti et forcé. Le pendule amorti et forcé est un modèle basé sur le pendule avec des modification pour gérer un amortissement, comme par exemple la résistance de l'air, et une force de forçage. on a donc l'équation : \[ \frac{\mathrm{d}^2\theta}{\mathrm{d} t^2} + \frac{1}{q} \frac{\mathrm{d} \theta}{\mathrm{d} t} + \sin(\theta) = g \cos(\phi) \] Où \(\theta\) est l'angle que forme le pendule par rapport à la normale. en posant la vitesse angulaire \(\omega = \frac{\mathrm{d} \theta}{\mathrm{d} t}\), on peut avoir \(\frac{\mathrm{d}^2\theta}{\mathrm{d} t^2} = \frac{\mathrm{d} \omega}{\mathrm{d} t}\) et on peut donc simplifier l'équation différentielle : \begin{align*} \frac{\mathrm{d}^2\theta}{\mathrm{d} t^2} + \frac{1}{q} \frac{\mathrm{d} \theta}{\mathrm{d} t} + \sin(\theta) &= g \cos(\omega_F t)\\ \frac{\mathrm{d} \omega}{\mathrm{d} t} + \frac{1}{q} \omega + \sin(\theta) &= g \cos(\omega_F t) \end{align*} Ce qui nous donne, en posant \( \) le système : \[ \left\lbrace \begin{matrix} \frac{\mathrm{d} \omega}{\mathrm{d} t} &=& - \frac{1}{q} \omega& - \sin(\theta) + g \cos(\phi)\\ \frac{\mathrm{d} \theta}{\mathrm{d} t} &=& \omega&\\ \frac{\mathrm{d} \phi}{\mathrm{d} t} &=& \omega_F& \end{matrix} \right. \] On a donc un système d'équation différentielles d'ordre 1 qui se résolvent très facilement numériquement.

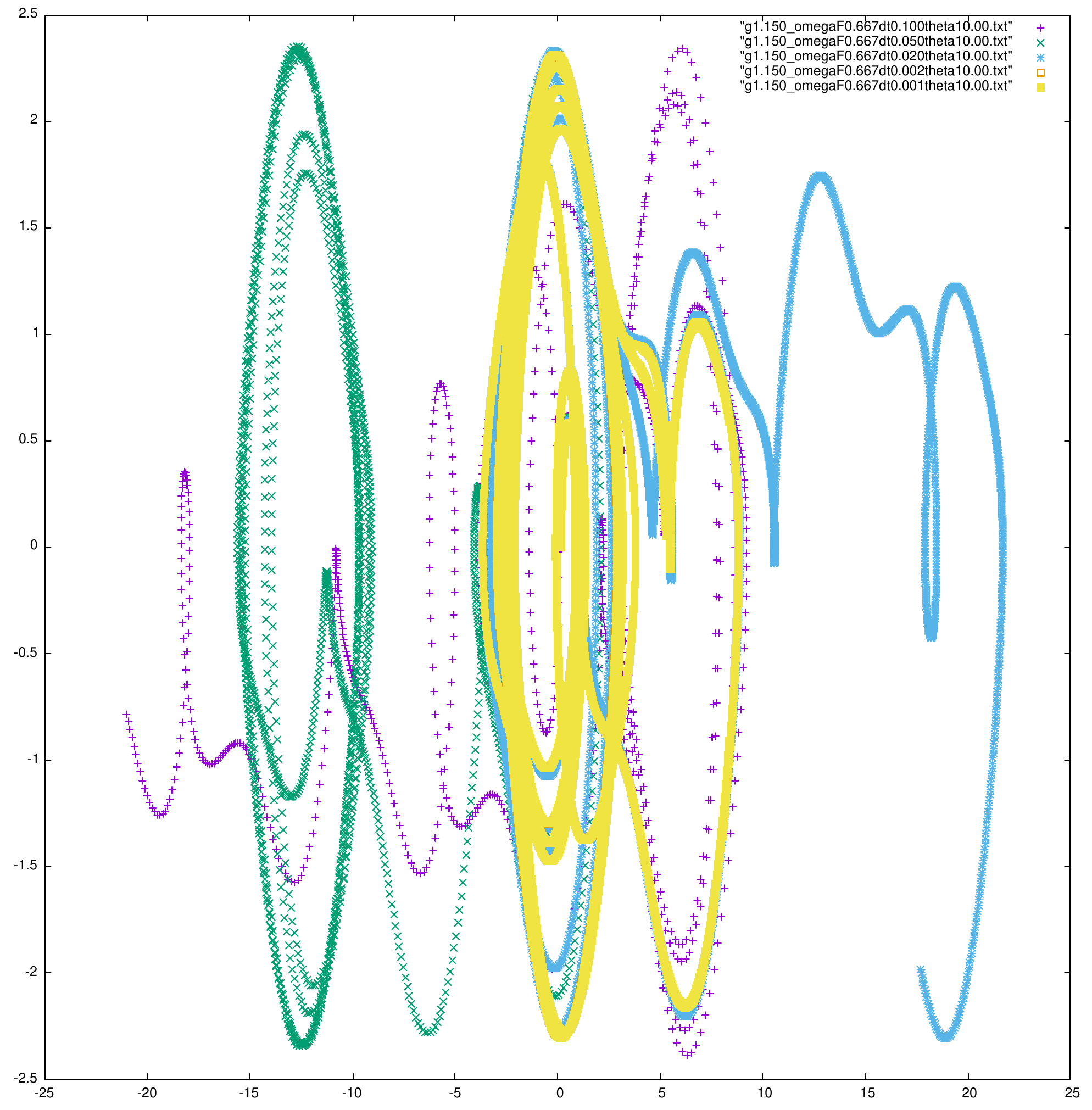
On peut s'intéresser à plusieurs scénarios, Dans un premier temps on s'intéresse à l'effet du pas de temps sur le système. Dans le diagramme de phase suivant, on place 5 système à des conditions initiales équivalentes, avec \( g = 1.15\), \(q = 2\), \(\omega_F = 2/3\), \(\theta = 10^o\), \(\phi = 0\), \(\omega = 0\), le seul paramètre qui change est le pas de temps, allant de \( 0.1s/points\) à \(0.001s/points\) :

On voit que malgré les conditions initiales identiques, les systèmes divergent significativement et ce, très tôt

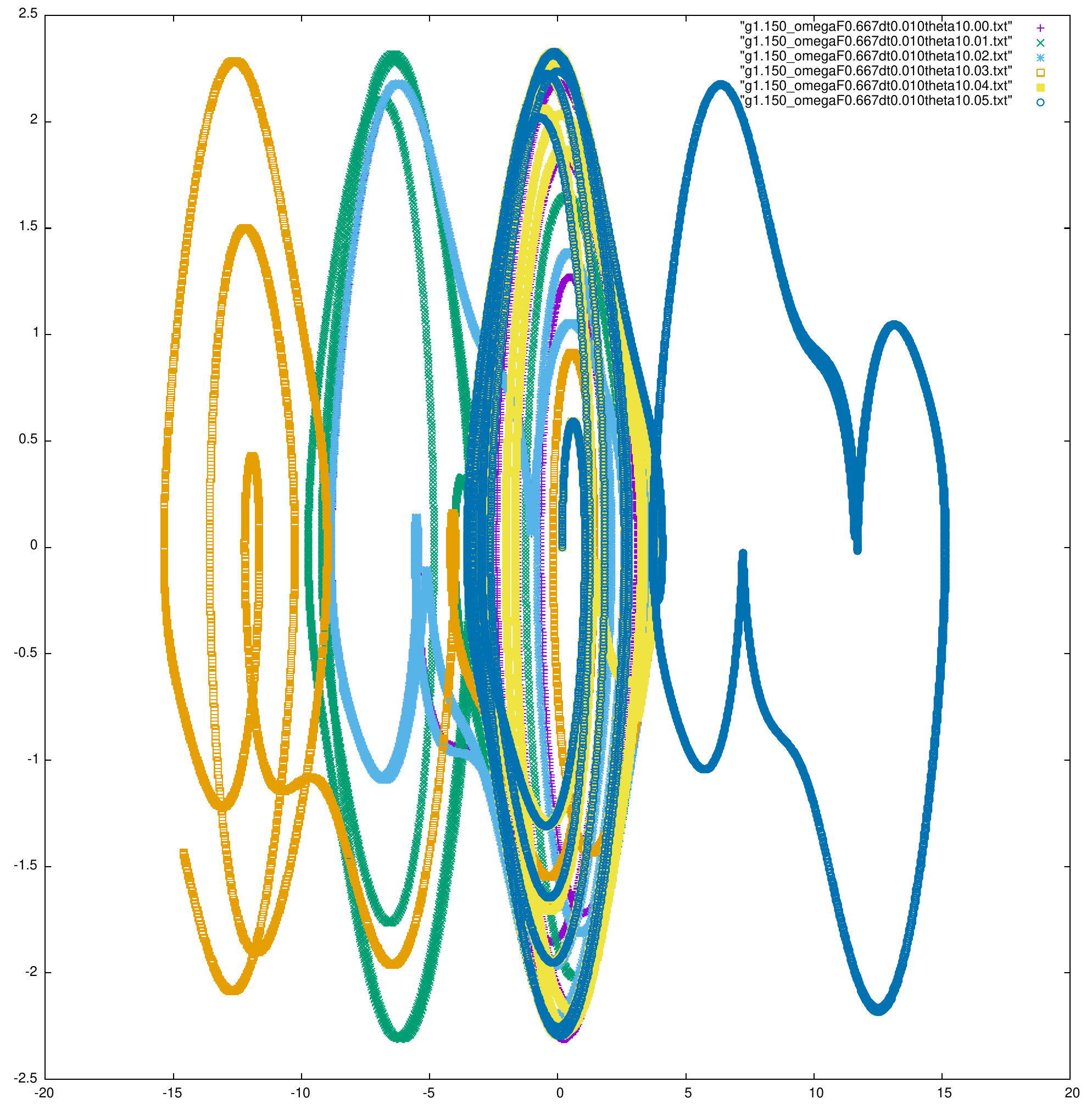
On s'intéresse maintenant, à l'effet du changement de \(\theta\) sur l'évolution du système, on prend donc des constantes équivalentes pour 6 systèmes, c'est à dire : \( g = 1.15\), \(q = 2\), \(\omega_F = 2/3\), \(\mathrm{d} t = 0.01s/points\), \(\phi = 0\), \(\omega = 0\). La seule différence entre les systèmes est le \(\theta\) initial qui a une différences de \(0.01^o\) entre chaque pendule :

On voit que les système divergent dans ce cas ici, cependant les systèmes mettent plus de temps à diverger que dans le cas où l'on change le \(\mathrm{d} t\) on a donc bien affaire à un système chaotique.

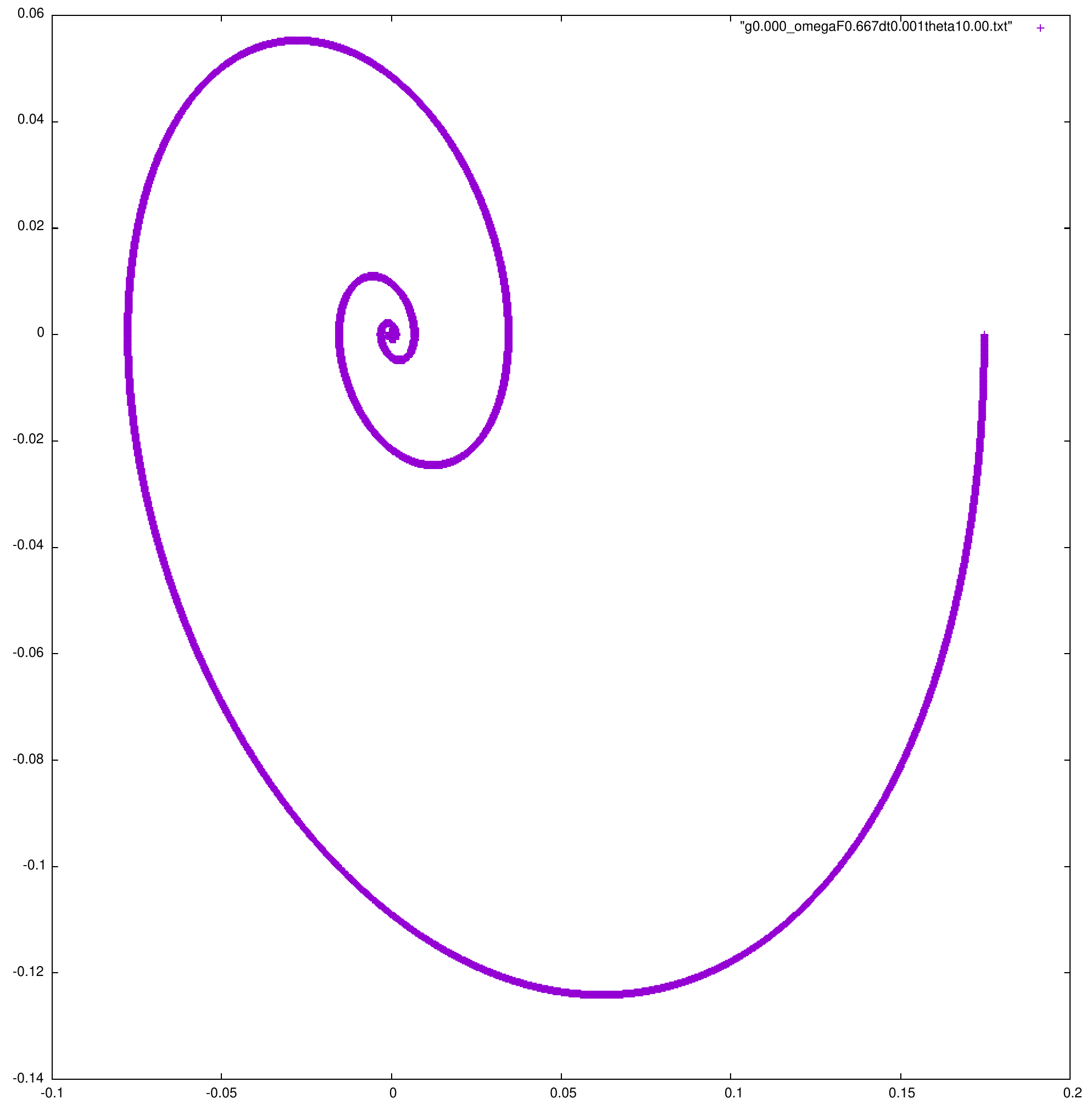
On peut désormais se mettre dans le cas \(g = 0\), avec les mêmes conditions initiales qu'auparavant, c'est à dire : \( q = 2\), \(\omega_F = 2/3\), \(\mathrm{d} t = 0.01s/points\), \(\theta = 10^o\), \(\phi = 0\), \(\omega = 0\)

On voit bien un attracteur, ce qui semble logique car dans le cas \(g = 0\) le sytème n'est plus forcé mais seulement amorti, donc le système tend vers l'équilibre.

On se place désormais, dans des cas avec \(g = 1.03\) et \(g = 1.04\) (avec les mêmes autres conditions initiales \( q = 2\), \(\omega_F = 2/3 \), \( \mathrm{d} t = 0.01s/points \), \( \theta = 10^o\), \(\phi = 0\), \(\omega = 0\).

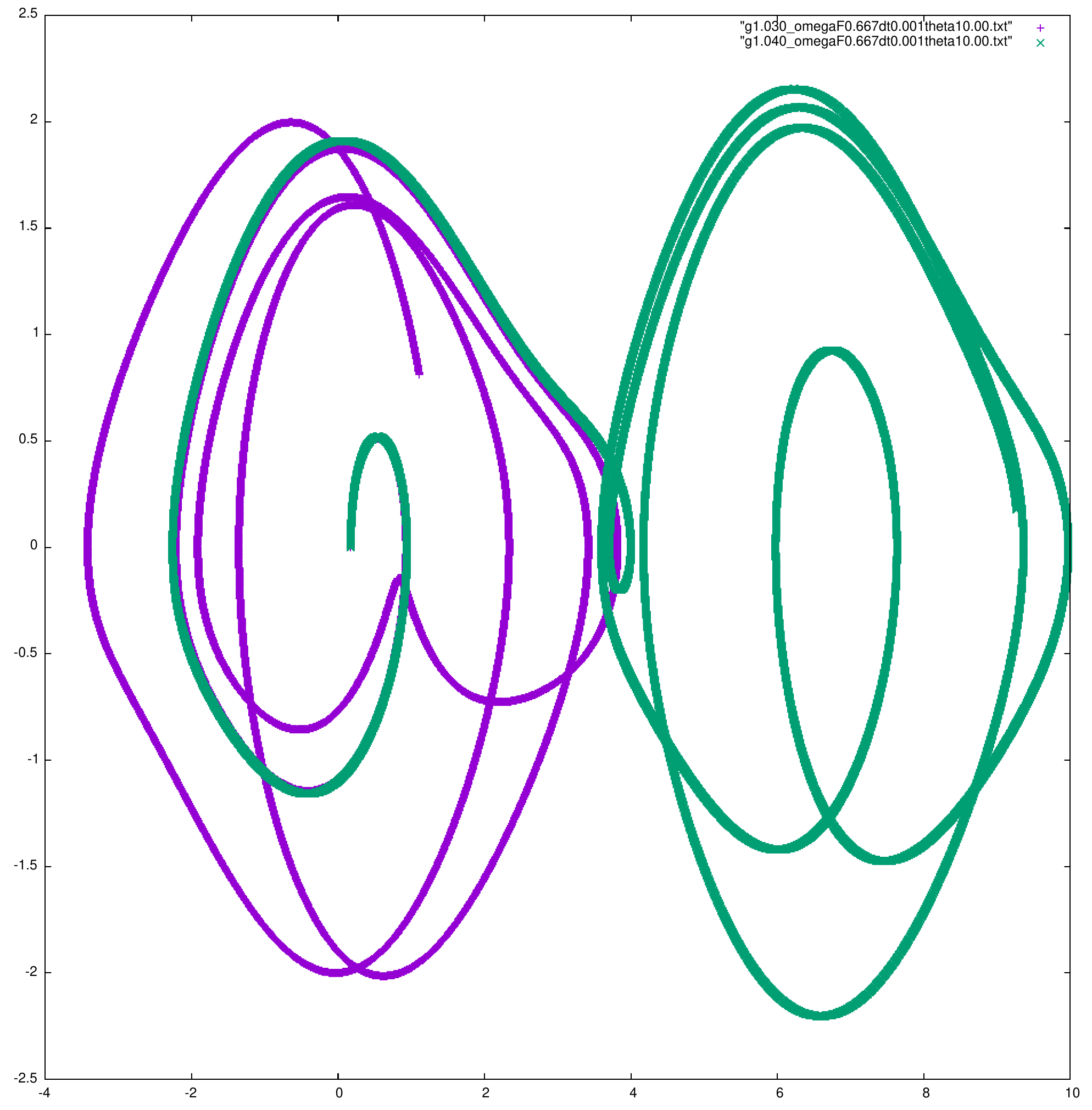
On voit que seul le cas \(g = 1.04\), on a la possibilité d'avoir un \(\theta > \pi \). On a donc dans le pendule qui fait un tour entier, on a donc un doublement de période.

On voit donc que le pendule amorti et forcé, comme le double pendule, est un système chaotique, de petites variations des conditions initiales mènent à des résultats drastiquement différents. Que ce soit la valeur de \(g\) choisie, la valeur de \(\theta\) choisie ou la valeur de \(\mathrm{d} t\) choisie.